Understand Features Machine Unlearning
Along with the data privacy becomes a global concern, many areas have legislated to protect user privacy, such as General Data Protection Regulation (GDPR) and the California Consumer Privacy Act (CCPA), etc. Therefore, machine unlearning grows into a popular direction of machine learning that has drawn a lot of attantion. In this artical, I’d like to share a paper, Machine Unlearning of Features and Labels.
Instance-based unlearning VS. Features unlearning
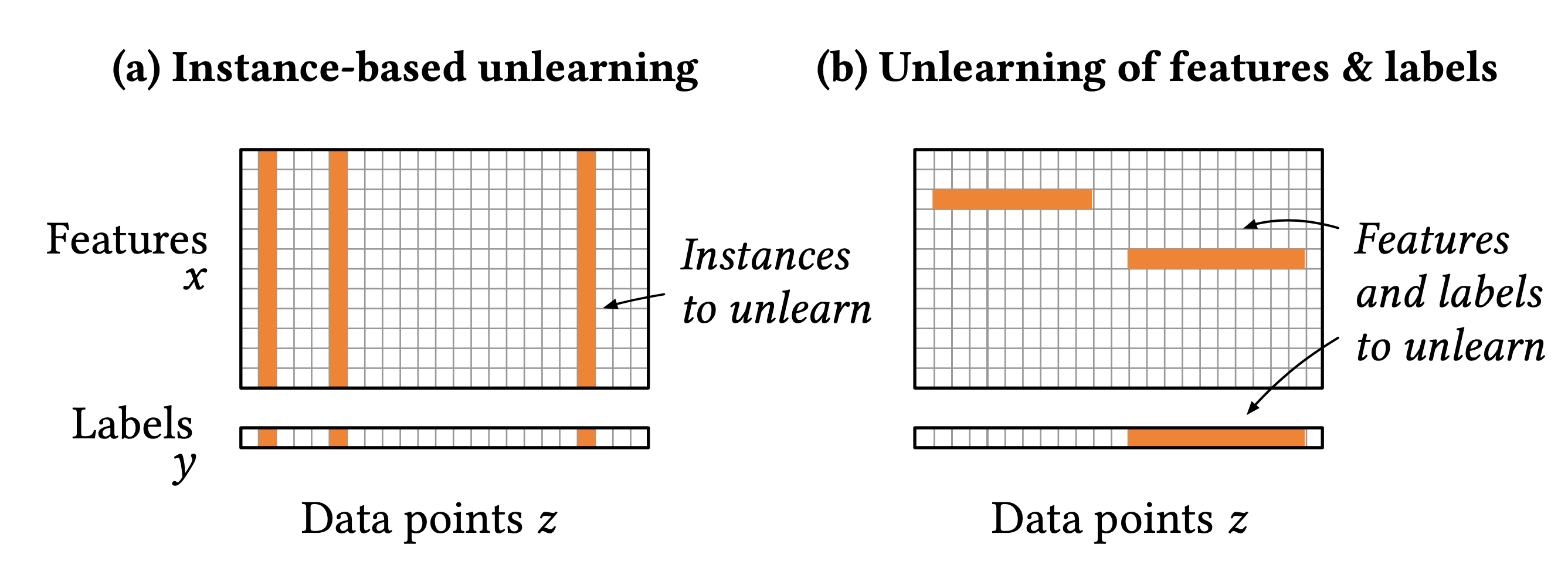
Previous studies of machine unlearning mainly focuses on instance-based unlearning. Specifically, those approaches aim to endow the ability of forgetting data points to a learned model. However, considering that a user only wants to revoke some sensitive attributes such as incomes or gender instead of all information, clearly instance-based unlearning methods is inappropriate. Therefore, we need to find a way that let machine learning models forget specific features of data points. In this paper, the authors proposed a method that targets on the unlearning features and labels. As shown in Figure 1, we can consider instance-based unlearning as a vertical unlearning, and unlearning of features and labels as a horizontal unlearning.
Influence Function
Another important concept in this paper is influence functions. The idea behind the influence functions is decompositing the objective function by upweighting the loss of a data point that want to forget with a small value. Formally,
\[\theta^*=\arg\min_{\theta}\frac{1}{|D|}L(\theta; D) + \epsilon \mathcal{L}(\theta; z),\]where \(L(\theta; D)\) denotes the objective function, \(z$& is the data point need to be forgotten. After a first-order Taylor expansion, we could get the influence of data point\)z$$. For more details please check this paper of Koh et al.
However, the influence of features and labels can not calculuate by dividing loss like that. The authors thus formulate unlearning of features and labels as
How would the optimal learning model \(\theta^*\) change, if only one data point \(z\) had been perturbed by some change \(\delta\)?
Hence, the new optimal model becomes
\[\theta^*_{z\rightarrow \tilde z}=\arg\min_{\theta}L(\theta, D)+l(\tilde z, \theta)-l(z, \theta),\]where they replace \(z\) by \(\tilde z=(x + \delta, y)\). Following the same idea of influence function, we upweight the changes and get
\[\theta^*_{z\rightarrow \tilde z}=\arg\min_{\theta}L(\theta, D)+\epsilon l(\tilde z, \theta)-\epsilon l(z, \theta).\]It is obvious that the above equation can be extend to a set of data points \(Z\) as well as the perturbed \(\tilde Z\) and obtain
\[\theta^*_{z\rightarrow \tilde z}=\arg\min_{\theta}L(\theta, D)+\epsilon l(\tilde Z, \theta)-\epsilon l(Z, \theta).\]Unlearning Features and Labels
In this section, I will introduce their approach to unlearning features and labels. Given a set of features \(F\) and the corresponding new values \(V\), they define perturbation on the affected points \(Z\) by
\[\tilde Z = \{(x[f]=v, y) : (x, y)\in Z, (f,v)\in F\times V \}.\]This equation tells us that \(\tilde Z\) is obtained by replacing the value of \(F\) with the new value \(V\). But, there is a gap between feature perturbation and feature revocation since we want models completely forget features. Obviously, feature revocation will change the dimension of input space as a result the dimension of parameter space will also change. Consequently, we can not use the influence functions. To address this problem, the authors present Lemma 1,
Lemma 1. For learning models processing inputs \(x\) using linear transformations of the form \(\theta^T x\), we have \(\theta^*_{-F}\equiv \theta^*_{F=0}\).
In other words, perturbing features with zeros is equivalent to revoking features. Concretely, to unlearning features \(F\), the perturbation data \(\tilde Z\) is obtained
\[\tilde Z=\{(x[f]=0, y): (x, y)\in Z, f\in F\}.\]Please note I did not discuss unlearning labels because it has the same procedure as unlearning features.